第2课数据结构_分类
热度🔥:212 免费课程
授课语音
数据结构分类
1. 介绍
常见的数据结构包括数组、链表、栈、队列、哈希表、树、堆和图，分为逻辑结构和物理结构。
1.1 逻辑结构
逻辑结构描述了数据之间的关系和组织方式，主要分为线性结构和非线性结构。
线性结构
线性结构中的数据元素按顺序排列，每个元素有且只有一个前驱和一个后继。主要包括：
数组（Array）：一组相同类型的元素，按顺序存储在内存中。支持随机访问，但插入和删除操作较慢，因为可能需要移动大量元素。
链表（Linked List）：由一系列节点组成，每个节点包含数据和指向下一个节点的指针。链表的变体包括：
- 单链表（Singly Linked List）：每个节点只有一个指针，指向下一个节点。
- 双链表（Doubly Linked List）：每个节点有两个指针，分别指向前一个节点和下一个节点。
- 循环链表（Circular Linked List）：链表的尾节点指向头节点，形成一个环。
栈（Stack）：遵循“后进先出”（LIFO）原则的数据结构。主要操作有推入（push）和弹出（pop）。
队列（Queue）：遵循“先进先出”（FIFO）原则的数据结构。主要操作有入队（enqueue）和出队（dequeue）。它的变体包括：
- 双端队列（Deque）：可以在两端进行插入和删除操作的队列。
- 优先队列（Priority Queue）：每个元素都有一个优先级，按照优先级顺序进行操作。
非线性结构
非线性结构中的数据元素没有线性排列的顺序，元素间的关系更加复杂。主要包括：
树（Tree）：一种分层的数据结构，包含节点和边。每个节点可以有零个或多个子节点。常见的树结构包括：
二叉树（Binary Tree）：每个节点最多有两个子节点（左子节点和右子节点）。
- 完全二叉树（Complete Binary Tree）：除了最后一层外，每层的节点都完全填满，最后一层的节点从左到右依次填充。
- 满二叉树（Full Binary Tree）：每个节点要么是叶子节点，要么有两个子节点。
- 平衡二叉树（Balanced Binary Tree）：每个节点的左右子树的高度差不超过某个阈值（通常为1）。
二叉搜索树（Binary Search Tree, BST）：二叉树的一种，其中左子树的值小于根节点的值，右子树的值大于根节点的值。
- AVL平衡树（Balanced Tree）：自平衡的二叉搜索树，任意节点的左右子树高度差不超过1。
- 红黑树（Red-Black Tree）：自平衡的二叉搜索树，节点颜色限制。
B树（B Tree）：自平衡的多路搜索树，适合存储和检索。每个节点可以有多个子节点，每个节点包含多个键（keys）和子节点指针。
B+树（B+ Tree）：B树的变体，所有键值都存储在叶子节点中，内部节点仅存索引。
堆（Heap）：一种特殊的完全二叉树，用于实现优先队列。分为最大堆（根节点最大）和最小堆（根节点最小）。
图（Graph）：由节点（顶点）和连接节点的边组成的结构。图可以是：
- 无向图（Undirected Graph）：边没有方向，连接两个节点。
- 有向图（Directed Graph）：边有方向，从一个节点指向另一个节点。
- 加权图（Weighted Graph）：边有权值，表示连接的代价或距离。
- 无权图（Unweighted Graph）：边没有权值，只有连接关系。
哈希表 是一种非常重要的数据结构，用于实现高效的插入、删除和查找操作。它通过哈希函数将数据映射到数组中的特定位置，以便在常数时间内完成这些操作。
图示
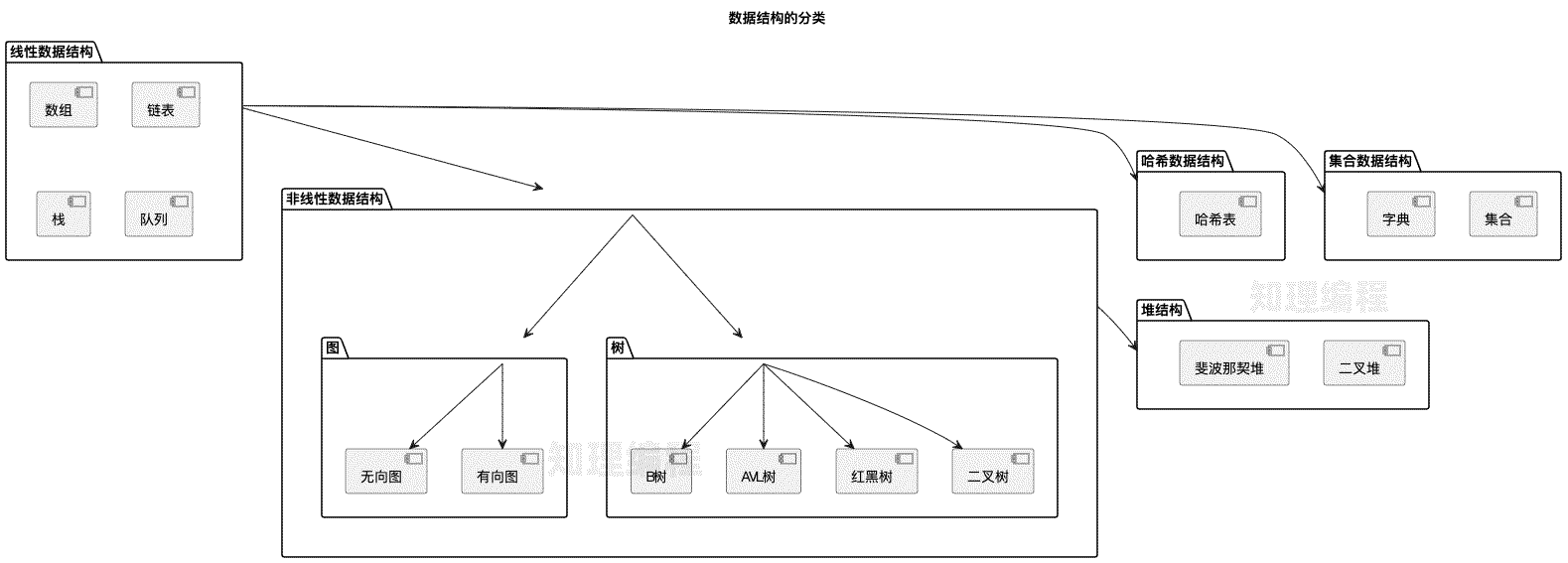
1.2 物理结构
物理结构描述了数据如何在计算机内存中实际存储。主要分为内存连续结构和内存分散结构。
内存连续结构：数据在内存中是连续存储的。主要包括：
- 数组（Array）：数据元素在内存中连续存储，支持快速随机访问。
内存分散结构：数据在内存中不是连续存储的，而是通过指针或引用连接起来。主要包括：
- 链表（Linked List）：节点在内存中分散存储，每个节点包含数据和指向下一个节点的指针（或双向链表中还包含指向前一个节点的指针）。
所有的数据结构都是基于数组、链表或两者的组合实现的。
2. 代码案例
# ======================线性结构==========================
# 1. 数组（Array）,提供了简单的设置和获取值的方法。
class Array:
def __init__(self, size):
# 初始化一个固定大小的数组
self.size = size
self.array = [None] * size # 初始化一个固定大小的数组，所有元素为 None
def set(self, index, value):
# 设置指定索引位置的值
if 0 <= index < self.size:
self.array[index] = value
else:
raise IndexError("Index out of bounds") # 索引越界异常
def get(self, index):
# 获取指定索引位置的值
if 0 <= index < self.size:
return self.array[index]
else:
raise IndexError("Index out of bounds") # 索引越界异常
def __repr__(self):
# 打印数组内容
return repr(self.array)
# 2. 链表（Linked List）,包括单链表、双链表和循环链表的基本实现。
# 2.1 单链表（Singly Linked List）
class Node:
def __init__(self, data):
# 节点的构造函数
self.data = data
self.next = None # 指向下一个节点的指针
class SinglyLinkedList:
def __init__(self):
# 初始化一个空链表
self.head = None
def append(self, data):
# 向链表末尾添加新节点
new_node = Node(data)
if not self.head:
self.head = new_node
return
last = self.head
while last.next:
last = last.next
last.next = new_node
def print_list(self):
# 打印链表中的所有节点
current = self.head
while current:
print(current.data, end=" -> ")
current = current.next
print("None")
# 2.2 双链表（Doubly Linked List）
class DoublyNode:
def __init__(self, data):
# 双链表节点的构造函数
self.data = data
self.next = None # 指向下一个节点的指针
self.prev = None # 指向前一个节点的指针
class DoublyLinkedList:
def __init__(self):
# 初始化一个空双链表
self.head = None
def append(self, data):
# 向双链表末尾添加新节点
new_node = DoublyNode(data)
if not self.head:
self.head = new_node
return
last = self.head
while last.next:
last = last.next
last.next = new_node
new_node.prev = last
def print_list(self):
# 打印双链表中的所有节点
current = self.head
while current:
print(f"{current.data}", end=" <-> ")
current = current.next
print("None")
# 2.3 循环链表（Circular Linked List）
class CircularNode:
def __init__(self, data):
# 循环链表节点的构造函数
self.data = data
self.next = None # 指向下一个节点的指针
class CircularLinkedList:
def __init__(self):
# 初始化一个空循环链表
self.head = None
def append(self, data):
# 向循环链表末尾添加新节点
new_node = CircularNode(data)
if not self.head:
self.head = new_node
new_node.next = new_node # 指向自身形成循环
return
last = self.head
while last.next != self.head:
last = last.next
last.next = new_node
new_node.next = self.head # 形成循环
def print_list(self):
# 打印循环链表中的所有节点
if not self.head:
print("Empty List")
return
current = self.head
while True:
print(current.data, end=" -> ")
current = current.next
if current == self.head:
break
print("(back to head)")
# 3. 栈（Stack），支持基本的推入和弹出操作
class Stack:
def __init__(self):
# 初始化一个空栈
self.items = []
def push(self, item):
# 推入栈
self.items.append(item)
def pop(self):
# 弹出栈顶元素
if not self.is_empty():
return self.items.pop()
raise IndexError("pop from empty stack") # 从空栈弹出异常
def peek(self):
# 获取栈顶元素但不弹出
if not self.is_empty():
return self.items[-1]
raise IndexError("peek from empty stack") # 从空栈查看异常
def is_empty(self):
# 判断栈是否为空
return len(self.items) == 0
def size(self):
# 返回栈的大小
return len(self.items)
# 4. 队列（Queue），支持基本的入队和出队操作
class Queue:
def __init__(self):
# 初始化一个空队列
self.items = []
def enqueue(self, item):
# 入队
self.items.append(item)
def dequeue(self):
# 出队
if not self.is_empty():
return self.items.pop(0) # 从队头移除元素
raise IndexError("dequeue from empty queue") # 从空队列出队异常
def is_empty(self):
# 判断队列是否为空
return len(self.items) == 0
def size(self):
# 返回队列的大小
return len(self.items)
# ======================非线性结构==========================
# 1. 二叉树（Binary Tree）
class TreeNode:
def __init__(self, data):
# 二叉树节点的构造函数
self.data = data
self.left = None # 左子树
self.right = None # 右子树
class BinaryTree:
def __init__(self):
# 初始化一个空二叉树
self.root = None
def insert(self, data):
# 插入节点（简单实现，按顺序插入）
if not self.root:
self.root = TreeNode(data)
else:
self._insert_rec(self.root, data)
def _insert_rec(self, node, data):
if data < node.data:
if node.left is None:
node.left = TreeNode(data)
else:
self._insert_rec(node.left, data)
else:
if node.right is None:
node.right = TreeNode(data)
else:
self._insert_rec(node.right, data)
def inorder(self):
# 中序遍历
return self._inorder_rec(self.root)
def _inorder_rec(self, node):
return self._inorder_rec(node.left) + [node.data] + self._inorder_rec(node.right) if node else []
# 2. 堆（Heap）
class MinHeap:
def __init__(self):
# 初始化一个空最小堆
self.heap = []
def insert(self, val):
# 插入值并调整堆
self.heap.append(val)
self._heapify_up(len(self.heap) - 1)
def _heapify_up(self, index):
# 调整堆，向上移动新插入的元素
parent = (index - 1) // 2
if index > 0 and self.heap[index] < self.heap[parent]:
self.heap[index], self.heap[parent] = self.heap[parent], self.heap[index]
self._heapify_up(parent)
def extract_min(self):
# 弹出最小值并调整堆
if len(self.heap) == 0:
raise IndexError("extract_min from empty heap")
if len(self.heap) == 1:
return self.heap.pop()
root = self.heap[0]
self.heap[0] = self.heap.pop()
self._heapify_down(0)
return root
def _heapify_down(self, index):
# 调整堆，向下移动根节点
smallest = index
left = 2 * index + 1
right = 2 * index + 2
if left < len(self.heap) and self.heap[left] < self.heap[smallest]:
smallest = left
if right < len(self.heap) and self.heap[right] < self.heap[smallest]:
smallest = right
if smallest != index:
self.heap[index], self.heap[smallest] = self.heap[smallest], self.heap[index]
self._heapify_down(smallest)
# 3. 图（Graph）
class Graph:
def __init__(self):
# 初始化一个空图
self.graph = {}
def add_edge(self, u, v):
# 添加边
if u not in self.graph:
self.graph[u] = []
self.graph[u].append(v)
def print_graph(self):
# 打印图的邻接表
for key in self.graph:
print(f"{key} -> {', '.join(map(str, self.graph[key]))}")
# 示例代码
if __name__ == "__main__":
# 测试数组
arr = Array(5)
arr.set(0, 10)
arr.set(1, 20)
print(arr)
# 测试单链表
sll = SinglyLinkedList()
sll.append(1)
sll.append(2)
sll.append(3)
sll.print_list()
# 测试栈
stack = Stack()
stack.push(10)
stack.push(20)
print(stack.pop())
# 测试队列
queue = Queue()
queue.enqueue(1)
queue.enqueue(2)
print(queue.dequeue())
# 测试二叉树
bt = BinaryTree()
bt.insert(5)
bt.insert(3)
bt.insert(7)
print(bt.inorder())
# 测试堆
min_heap = MinHeap()
min_heap.insert(3)
min_heap.insert(1)
print(min_heap.extract_min())
# 测试图
g = Graph()
g.add_edge(1, 2)
g.add_edge(1, 3)
g.print_graph()
3. 总结
本文概述了常见的数据结构及其分类，分别介绍了逻辑结构和物理结构，并通过代码示例展示了各种数据结构的基本实现。掌握这些数据结构将有助于高效地处理和存储数据。
系列课程：
📱 下载客户端
小程序
安卓APP
iOS APP
📚 视频课程
- Java入门教程 86
- Python入门教程 33
- JavaScript入门教程 35
- C++入门教程 45
- Go入门教程 38
- 数据结构与算法 30
- 设计模式入门 23
- SQL入门教程 29
- C语言入门教程 25
- TypeScript入门教程 19